1. 上次的讨论结果

1. 计算建模：下一步了解间歇计算里面的能量开销的问题（比如，能量开销取决于间隔时间，但是间隔太大会导致sisyphean execution，太小会导致能量开销过大）是如何建模的，从定性到定量。
2. 通信建模：了解通信中的 EH-Optimized Transmission 是如何建模的，高级任务：了解清楚为什么要使用强化学习和凸优化等工具，何时用这些工具。
3. 了解反射式无线电的挑战和如何建模的。
4. 新的话题：通信和计算耦合的情况下如何建模。
5. 每天知道自己在干什么，要干什么，做了什么。

这次的任务就是完成第一条。

2. 间歇计算

Why:EH-IoTs 的能量供应是不确定的，易失性存储器显然在掉电后会丢失数据，因此必须周期性地将易失性状态保存在非易失性存储器中，这一技术称为checkpointing。当电能恢复时，程序可以从最近保存的状态中重新开始。但是 checkpointing 效率低下，不能直接用于间歇计算。

Challenge：能量开销；Sisyphean execution；状态不一致；时序不一致。

Solving Direction：1. 检查点的预置与激活；2. 能量不足时checkpointing，之后立刻休眠。3. 基于任务流的编程方式。4. 看门狗checkpointing，引入定时器中断。5. 断电重启后确定设备当前时间，保证当前时间与世界时间一致非常重要。现有的方法包括：SRAM和电容的剩磁衰减来估计时间。

我的目标是，找到上述过程蕴含的优化问题，并了解其是如何建模的。

3. 建模1

“Idetic: A High-level Synthesis Approach for Enabling Long Computations on Transiently-powered ASICs”

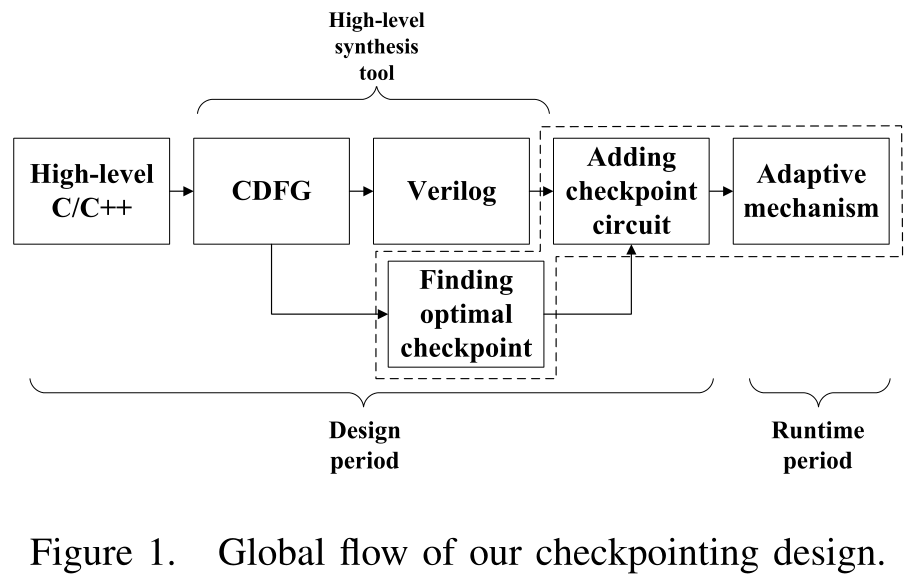
Find optimal checkpoint：

目标：在具有能量收集源的 ASIC 上运行长时间的应用程序。

已知：ASIC的高级综合设计。能量收集平台的特性。在实验平台上的关于电容器特性的信息。

问题：寻找插入检查点的最优位置，使能量开销最小，并最大限度地减少停电时的重新计算能量成本。

计算 $\operatorname{Cost}\left(e _{s _{i} s _{j}}\right)$：

以下是程序的CDFL输出文件，以及有限状态机信息。

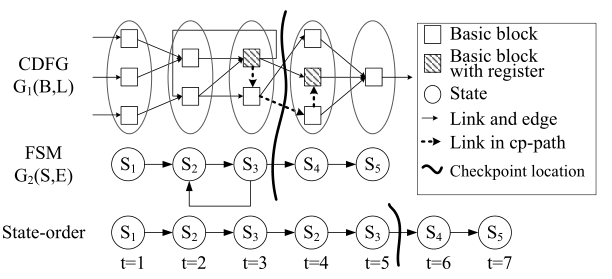
其中，$B=\{b _{1}, \ldots, b _{N}\}$ 是 basic-block 的集合（加法器，乘法器，条件器），$L$ 是链路（通过basic block的数据流）的集合。CDFG图用 $G _{1}(B, L)$ 表示。

同样的，对于FSM图，用 $G _{2}(S, E)$ 表示。其中，$S =\{s _1,\cdots,s _M \}$ 是状态的集合，$E$ 是指示状态之间的转变的链路集。每一个 $B$ 中的节点属于 $S$ 中的一个状态。一些basic-block包含一个寄存器，用来保存basic-block的输出。为了跟踪寄存器，我们定义了一个逻辑函数，$P(b _n,b _m)$，其中 $b _n,b _m \in B$。当满足下述条件时，$P(b _n,b _m)$ 输出 1，否则输出 0。

1. $b _n$ 有寄存器。
2. 在 $b _n$ 和 $b _m$ 之间有一条路径，使得该路径中的基本块(除了 $b _n$ 和 $b _m$ 之外)都没有寄存器。如果这样的路径存在，则寄存器 $b _n$ 应该被存储。我们称这样的路径为 $cp-path$。

设置检查点的开销由当前状态下恢复所需存储的寄存器的数量决定，根据下图计算：

我们用开销 $\operatorname{Cost}\left(e _{s _{i} s _{j}}\right)$ 表示在给定先前状态为 $s _i$ 的情况下在状态 $s _j$ 设置检查点所需的位数。

首先，我们在集合 $\Phi$ 中列出来应该被存储的 basic-blocks（我理解的 basic-block 就是带有数值结果的运算器。）对于 $E$ 中的一条链路，$e _ {s _{i} s _ {j}}$，我们首先设 $\Phi$ 为空。（Line 1-2）。接下来，我们将在 $s _j$ 之前开始并在 $s _j$ 之后结束的CP路径的所有基本块添加到$\Phi$，反之亦然(第3-9行)。如果 $e _{s _i s _j}$ 是一个循环链路，我们还将所有从 $s _j$ 和 $s _i$ 之间的一个状态开始，并在 $s _j$ 结束的 $cp-paths$ 中的所有基本块加进去。（Line 10-14）。最后，为了计算检查点的开销，我们将 $\Phi$ 中所有寄存器的宽度相加(第15-17行)。开销成本 $\operatorname{Cost}\left(e _{s _{i} s _{j}}\right)$ 根据表三的性质转换为能量成本。

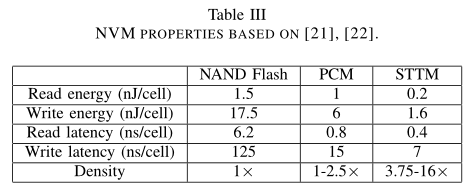
为了找出每个状态下的计算能量开销，我们使用Synopsys Design Compiler进行了功耗仿真。

3.1 设计时定位

checkpointing 方法（动态规划）：

为了找到最佳检查点位置，IDETIC需要知道状态的执行顺序，我们称之为状态顺序。状态顺序是通过展开有限状态机并将其转变为非循环的状态序列来导出的。我们在ModelSim中进行了RTL级的仿真，以求出状态顺序。

约束：

1. 两个连续的checkpoint的距离受到限制，最大距离不能超过 $D _ {max}$。
2. 所有检查点所产生的能量开销最小。

目标：插入检查点，使得完成状态顺序中的所有T个状态的总能量最小。总能量指的是计算能量和检查点开销能量。

目标函数($OF$)由 $C _{O F}(t, k)$ 表示，是在状态顺序的第 $t$ 个状态结束时完成总共 $k$ 个检查点的总能量。成本 $C _{CP}(t)$ 对应 $\operatorname{Cost}\left(e _{s _{i} s _{j}}\right)$ ，其中 $s _i$ 是第 $t-1$ 个状态，$s _j$ 是第 $t$ 个状态。$C _{CO}(t)$ 是从开始到第 $t$ 个状态的总的计算消耗能量。

参数：

我们利用动态规划来寻找检查点位置。该算法如伪码-2所示。初始条件设置为确保第一个检查点位于距起点(第1-5行) $D _{max}$ 的最大距离。用$K _{max}$表示满足以下条件的检查点数目的一个上界：$K _{max}>\frac{T}{D _{max}}$。在 $t$ 处插入第 $k$ 个检查点的最小成本包括在该点设置检查点的成本(第8行)加上第 $t$ 个状态之前消耗的最小总能量(第9行)。

3.2 自适应在线学习

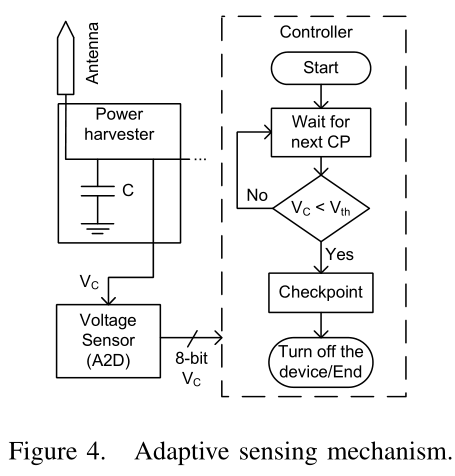
然而，上述设计时定位的检查点策略在输入能量足够的情况下可能效率不高。为了应对电源能量的变化，我们提出了一种自适应在线机制，通过A/D转换器读取电容器的电压，在每个检查点之前感知可用存储能量。如果电容器的能量水平(对应于 $V _c$ )大于两个连续检查点之间的最大能耗，则跳过检查点；在我们的目标应用中，两个连续检查点之间的最大能耗(对应于 $V _{th}$ )是通过功率模拟离线测量的。否则，我们完成预定的检查点并关闭设备以降低重新计算成本，如下图所示。我们假设平均输入功率远低于平均应用程序功耗。这一假设对于几种能量容量和充电率有限的能源回收源是现实的。

4. 建模2

原文：“PATH: Performance-Aware Task Scheduling for Energy-Harvesting Nonvolatile Processors”

与 建模1 不同，这篇文章不设置checkpoint，程序的执行遵循任务流 $^{1,2}$，任务通过控制流图连接，可以消除数据不一致的问题，具体来说，变量被定义为本地任务变量和全局任务变量，前者仅限于本任务使用，且存储在RAM中，而后者可以被其他任务使用，且存储在ROM中。由于任务是等幂的，且输入存储在ROM中，因此断电时产生相同的结果，从而保持数据一致。

背景：

我们知道EH-IoTs的电源供应是不稳定的，阻碍了任务的执行。为了保证任务的顺利进行，人们设计了许多非易失性处理器（Nonvolatile processors，NVPs），通过集成分布式 NVP 元件（如非易失性D触发器和非易失性静态随机存取存储器，这些非易失性元件可以支持即时和高效的片上备份和恢复操作），这些NVPs可以对在断电之前在其上执行的任务进行快照，使得它们可以在电源恢复之后以可以忽略的开销继续工作。虽然 NVP 显著降低了不可靠电源下计算的电源切换开销，但涉及处理器与外设之间的 I/O 操作和传感器上的传感操作的任务在电源中断时仍不能存储状态，从而导致较高的电源切换开销并降低了 EH-IoTs 的整体性能。（电源切换开销：当前功率脉冲无法支撑到某个任务的结束，任务执行失败，下一个功率脉冲时，如果任务需要回滚与重新初始化，会导致相当大的能量和时间损失。一般来说，涉及易失性外设的任务会遇到较大的能量切换开销，而其他任务的开销非常小，因为基于NVPs）

即使许多研究者已经从硬件级别提出了一些外设的非易失性 I/O 结构，但是仍然需要任务调度方案来避免通用易失性外围设备不必要的回滚和初始化。

现有的研究方法中，根据单个任务在执行过程中是否可以被中断和调度，它们大致分为两类：任务间调度和任务内调度。

任务间调度将任务看作不可分割的单元，如果中断后需要重新执行，相关研究的学者致力于寻找任务级的自适应方案。

任务内调度任务可以再细分，通过中断执行中的任务来进一步提高性能，并根据功率插入其他任务来执行。

传感器节点的典型任务流程通常涉及数据采集、数据处理和数据传输，随时可能发生断电。而涉及外设的任务（例如，感测、存储器访问和传输操作）不能被备份，因此在发生回滚时会导致相当大的时间和能量损失，因此作者的研究目的是：研究任务内调度方案，以避免易失性外围设备不必要的回滚和初始化。

作者提出了一种考虑任务分割的性能感知任务调度方法。

1. 分析任务的电源切换开销，并将考虑电源切换开销的路径问题形式化为混合整数线性规划（MILP）问题：同时考虑了时间和功率约束，目标是最大限度地减少所有任务的完成时间。（NP完全问题）

2. 在此基础上，提出了基于任务分割(TS)策略的离线启发式调度算法，有效地解决了该调度问题。（是先有任务分割，然后因为MILP问题计算量过大，所以需要启发式学习算法）

3. 对调度问题进行了理论分析，给出了用解析表达式估计解的方法。在此基础上，提出了一种基于离线优化参数的在线性能感知启发式调度算法。

离线和在线的区别就是是否根据当前采集的能量水平动态决定最优调度结果。在线算法基于对历史功率轨迹的分析来预测未来功率脉冲的幅度和持续时间。

4.1 问题描述

电源切换开销定义为因电源中断导致的回滚、备份和恢复而导致的额外操作时间/能量。根据任务在断电后是否可以恢复，将任务分为两类：

• 可以恢复的任务具有低的电源切换开销，称为LS任务。
• 不能恢复的任务具有高的电源切换开销，称为HS任务。

挑战：一些HS任务在断电后需要重新执行以保证正确性，导致电源切换开销非常大。

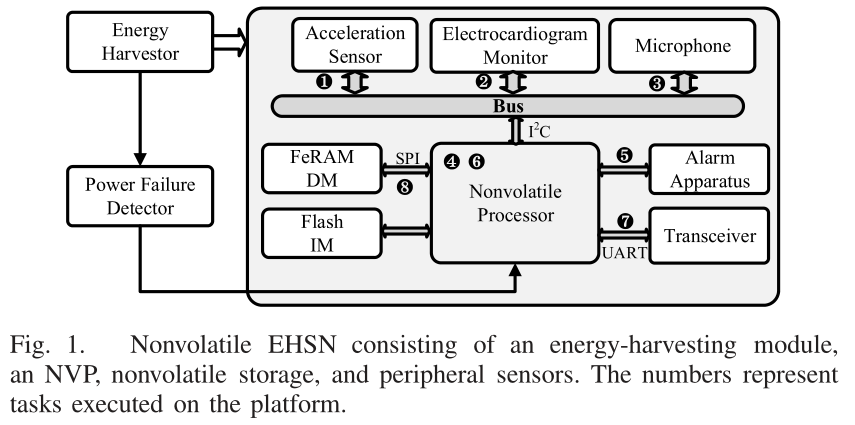
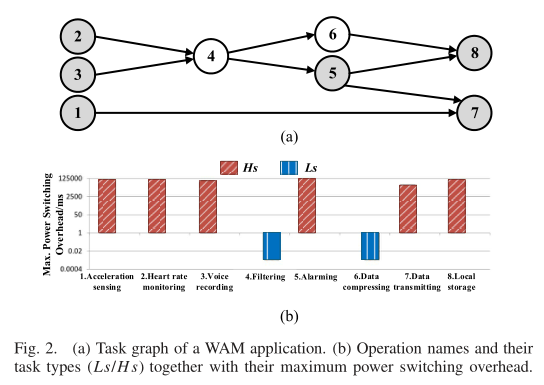
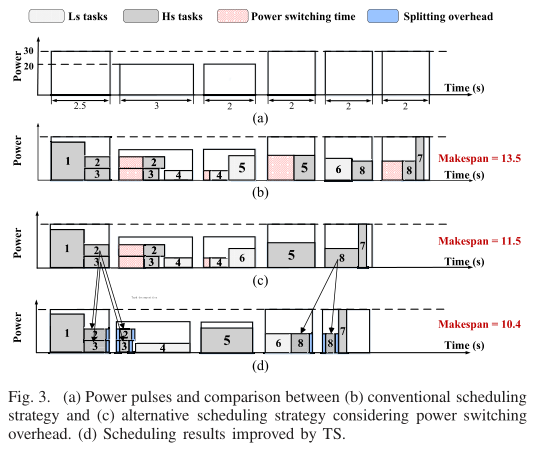
图三(a) 对应供能脉冲，(b,c,d)的任务功率必须低于供能功率，用完成所有任务的总时间来表征三种方法的性能。(b)对应传统方法，(c)考虑了电源转换开销，(d)基于任务分割(TS)策略。

上面的例子表明，考虑到电源切换开销的限制，调度策略的挑战在于如何将任务与功率脉冲的功率和时间相匹配。调度策略应该平衡任务依赖、并行度、拆分粒度和任务类型。

4.2 建模

变量：

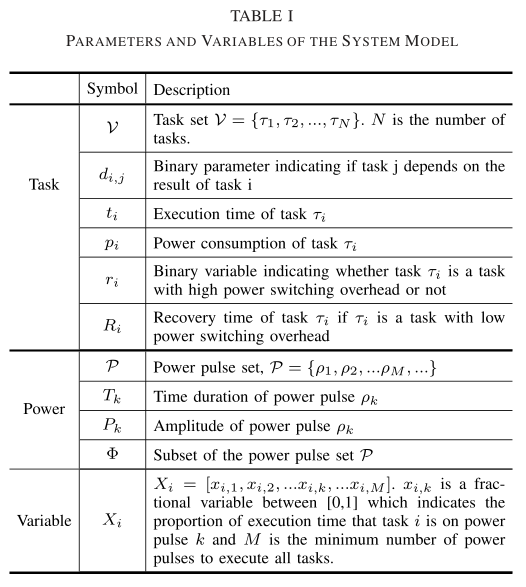
调度目标：

通过将每个任务映射到一个或多个功率脉冲来最小化所有任务的总执行时间。等价于找到完成所有任务的最小功率脉冲数量。

其中，$M$ 是使用的功率脉冲数。$\rho _{i}$ 是第 $i$ 个功率脉冲，$\Phi$ 是消耗的功率脉冲集。因为时间连续性，$\rho _{k} \in \Phi$ 一定是在 $\rho _{k-1} \in \Phi$ 的基础之上的。

定义1：

(尾函数) $g _{e}\left(X _ {i}\right)$ 返回输入向量的最后一个非零元素的位置。

\[\tag{2} g _{e}\left(X _{i}\right)=\max \left\{k \mid \sum _{j=k}^{M} x _{i, j}>0, k \in[1, M], k \in Z\right\} , \forall i \in[1, N]\]

尾函数 $g _{e}\left(X _ {i}\right)$ 与变量 $x _{i,j}$ 非线性相关。通过引入下面的中间变量，将复杂度降低为线性。

根据 $A$ 和 $A^{\prime}$，很容易定位 $X _{i}$ 的第一个和最后一个非零元素。例如，

$X _{i}=[0,0,0.3,0.7,0,0.2,0]$，有 $A _{i}=[0,0,0.3,1,1,1.2,1.2]$ 和 $A _{i}^{\prime}=[1.2,1.2,1.2,0.9,0.2,0.2,0]$。

为了表示 $g _{e}\left(X _ {i}\right)$ 和必要的约束，我们引入了三个逻辑变量 $\beta _{i, k}, \beta _{i, k}^{\prime}$ 和 $\gamma _{i, k}$ 以表示 $\alpha _{i, k}, \quad \alpha _{i, k}^{\prime}$ 和 $x _{i, k}$ 是否为正数（正数对应 1）。

其中，$N _1,N _2,N _3$ 是充分大的数。

因此，尾函数 $g _{e}\left(X _ {i}\right)$ 可以线性表示如下：

目标函数（式 $(1)$）最小化了消耗的功率脉冲数，也就是最小化了最后一个任务的结束位置：

为了将目标函数写为线性形式，引入了变量 $Y$：

因此，$(6)$ 式可以写为

约束包括电源切换、时间、能量和功率峰值限制。

1. 电源切换约束：

HS任务的电源切换开销很高，因此HS任务应该在不中断电源的情况下执行，这意味着它们应该只映射到一个功率脉冲，即

对于执行时间超过功率脉冲持续时间的任务，显然不满足上述约束，此时后续所有依赖于这一任务的结果的任务也无法执行。后面介绍的任务分解（Task Splitting, TS）策略可以解决这一问题。

2. 时间约束：

$(10)$ 描述了任务的依赖关系。$M-\sum _{k=1}^{M} \beta _{j, k} +1$ 表示任务 $\tau _{j}$ 的开始执行时间，当变量 $d _{i j}=1$ 时，$\tau _j$ 的开始时间不能比 $g _{e}\left(X _{i}\right)$ 小，意思是任务 $\tau _j$ 只能等任务 $\tau _i$ 执行完成后才能执行。

$^{\text{注意：原文中公式不同，我觉得错了，上面的是改正后的。}}$

等式 $(11)$ 表示任务 $\tau _i$ 的总执行时间等于在任务 $\tau _i$ 上花费的每个功率脉冲的执行时间之和。如果 $\tau _i$ 是具有低功率切换开销的任务，则应该将 $R$ 倍的中断次数加到总执行时间中。

3. 峰值功率约束：

任务 $\tau _i$ 的功率必须低于所在功率脉冲的功率。

4. 能量约束：

由于任务通常在不同的外设上执行，并且可以并行执行，所以我们没有限制每个功率脉冲下的任务数量。因此，能量约束用于确保所有执行任务消耗的总能量应低于每个功率脉冲提供的能量，如下式所示：

注意，$(12)$ 仅限制每个功率脉冲下的任务的功率幅度，而 $(13)$ 中的每个功率脉冲的能量决定任务的最大并行度。

MILP 实现：LINGO

4.3 启发式离线调度策略

众所周知，第二节中的 MILP 公式计算密集且不可伸缩。由于 TS 可以通过将 HS 任务分解成小任务来进一步缩短总任务执行时间，并生成大量新的任务组合，因此将有更大的设计空间可供探索，这对于 MILP 求解器来说是不可接受的。因此，作者提出了一种启发式算法来解决调度问题。

任务分解策略：

电源切换开销是由意外电源故障引起的，主要由重新初始化和执行回滚的额外操作时间/能量组成，而 TS 开销是由有意的任务分解引起的，只需要额外的重新初始化。相比之下，TS策略降低了长时间执行回滚的可能性，从而降低了总体电源切换开销。

假设 TS 开销为 $S$（通过参考实际的 HS 任务的初始化时间获得）。为了简单起见，均匀分解任务。例如，将 $t _i$ $k$ 等分，可以得到小的 HS 任务的执行时间为 $t _{i}^{\prime}=\left(t _{i} / k\right)+S$。直观地说，如果 $k$ 太大，则会导致更大的分裂开销。但是，如果 $k$ 太短，则不能提供足够的性能改进。因此，每个任务都有一个最佳的拆分粒度。选择分裂粒度时主要考虑了三个影响因素：任务长度，功率脉冲的平均长度，功率波动率。

算法框架：

TS 分解之后，下文表述的 HS 任务均为拆分后的小任务。

更高效的启发式算法：减少MILP公式中的变量数目，作者提出了一种贪婪方法来填充功率脉冲。

定义2：

每个功率脉冲的功率利用率： 给定功率脉冲 $\rho _{k}$（时间 $T _k$，振幅 $P _k$），备选任务集 $\mathcal{V} _{\text {can }}=\{\tau _{i _{1}}, \tau _{i _{2}}, \ldots, \tau _{i _{n}}\},\mathcal{V} _{\text {can }} \in \mathcal{V}$。功率利用率（表示为 $U$）被定义为有效执行的任务消耗的能量与功率脉冲组提供的总能量之比。它可以表达为：

\[\tag{14} U=\frac{\sum_{n} x_{i_{n}, k} T_{k} p_{k}}{P_{k} T_{k}}, \quad i_{n} \in[1, N], k \in[1, M]\]

所谓贪婪启发式算法，就是根据功率脉冲的条件选择性地优先执行 HS 任务：

算法1：基于 TS 算法的启发式任务调度算法 $K _{\min }=F(\mathcal{V}, \Phi)$ $^{\text{按照我的理解，第12行的MILP的任务集应该是在前面的 $\mathcal{E}$ 基础上加入了所有 $\mathcal{V} _{\text {can }}$ 中的 LS 任务。}}$

算法2：$\mathcal{V} _{\text {can }}$ 的选择，$\mathcal{V} _{\text {can }}=\operatorname{Cand}\left(\mathcal{V}, \rho _{m}\right)$

算法1的大循环（Line 2）遍历了所有HS任务分解策略，在循环内部，程序为每个功率脉冲选择合适的任务，直到所有任务完成。第六行通过算法2选择候选任务集。算法2的任务选择算法的原理是：

如果 HS 任务的最早完成时间早于功率脉冲结束时间， LS 任务的最早开始时间早于功率脉冲结束时间，则将 HS（LS）任务添加到当前功率脉冲对应的候选集中。（因为 HS 任务不能中断，而 LS 任务可以中断后接着运行。）

第 7-11 行将高优先级分配给能在当前功率脉冲内完成的 HS 任务。第12行通过求解本地MILP算法选择任务。由于减少了优化变量的数量，使得计算复杂度 $O^{\prime}$ 与原MILP算法相比呈指数下降。

4.4 考虑电源切换开销的任务调度理论分析

在这一部分中，作者从理论上研究调度所需的最小功率脉冲数。它主要用于提供对执行时间的快速评估，并指导在线调度策略的设计。首先分析 HS 任务的特点，然后计算这些任务所需的最小功率脉冲数。在此之后，加入 LS 任务以获得总的最小功率脉冲数。

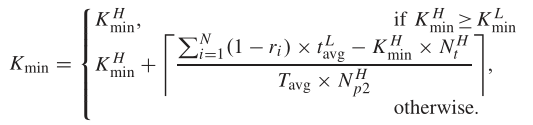
4.5 在线调度策略

离线策略分析了历史功率轨迹和任务的特点，给出了任务调度的通用参数设置，并提出了一种在线性能感知策略，利用这些优化后的参数，根据当前采集的能量水平动态决定最优调度结果。

概述：

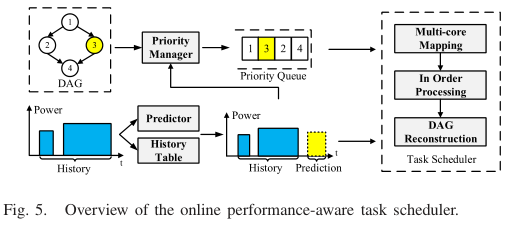
图5描述了在线调度器的概况。每次电源脉冲开始时，整个过程都会被触发。它由三个主要部分组成：优先级管理器、能源预测器和任务调度器。一个具有历史功率幅度和历史持续时间的历史表被维护以辅助预测和任务调度算法。优先级管理器首先根据功率预测结果和任务的DAG给出所有剩余任务的优先级顺序。然后，将所有任务按优先级排序，放入任务队列。然后，调度程序将任务映射到具有功率约束的传感器节点上，并按优先级顺序进行处理。

能源预测

当前的功率脉冲 $\rho _{k}$ 的历史表：$\mathcal{H} _{k}=\{\rho _{k-N _{\text {his }}}, \rho _{k-N _{\text {his }}+1}, \ldots, \rho _{k-1}\}$

用线性加权移动平均估计出平均功率幅度和持续时间：

历史表还可以预测是否即将到来的 HS 任务可以被执行，原理是计算历史数据中可以覆盖 $\tau _{i}$（HS 任务长度）的功率脉冲比例。

其中，$I(\bullet)$ 是指示器，如果参数为真就输出1，否则输出0。

任务优先级分配：

当任务的所有父节点都完成时，它就变成可执行的。当传感器节点处于空闲状态时，通常会有多个任务等待执行。优先级算法需要考虑当前能源条件、任务依赖关系和任务类型。其优先级是用权重来衡量的：

1. 考虑哪种类型的任务（HS 或 LS 任务）支配着执行时间，这一权重称为支配权重 $w _d$
2. 如果预测的功率脉冲持续时间大于 HS 任务的长度，则 HS 任务的优先级应高于 LS 任务，以避免后续掉电导致回滚。它被称为 HS 权重 $w _h$
3. 关键路径上的任务应该具有更高优先级，因为他们完成后可以增加更高的并行度。它被称为关键权重 $w _c$

根据理论分析，在算法3中设计并给出了一种在线任务优先级算法。

1
2
A. Colin and B. Lucia, "Chain: Tasks and channels for reliable intermittent programs," ACM SIGPLAN Notices, vol. 51, no. 10, pp. 514–530, 2016.
K. Maeng, A. Colin, and B. Lucia, "Alpaca: Intermittent execution without checkpoints," in Proc. ACM Program. Lang., vol. 1, 2017, p.96.

• Previous
  Sensing, Computing, and Communications for Energy Harvesting IoTs的第一次在线讨论
• Next
  文献检索与信息分析课程